Problem 15: Lattice Paths
Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
How many such routes are there through a 20×20 grid?
This is a special one, because we don’t need to write any code to solve it!
(That’s probably true for many of the others but I actually know how to do it for this one)
We can utilize properties of combinatorics to find the solution. First, let’s consider a much more managable grid to better understand the problem. I’ll use a grid with 2 different dimensions to make things more clear, but this works for a rectangular grid of any size or proportion.
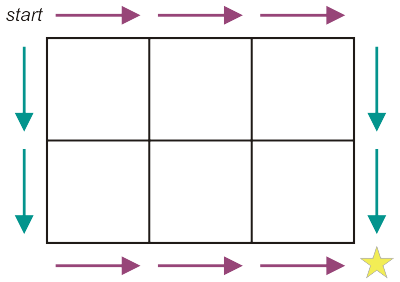
In this 2x3 grid, we know that no matter which path we choose, we must ultimately move right three times and down two times to reach the bottom right corner and get that enticing gold star.
At this point, we can convert our moves into a much simpler format for solving: a string! The path is always \(2+3=5\) moves long, so the string is 5 characters long. We can use R for a move right and D for a move down.
RRRDD
If we had our 2 characters, R and D, and we could always choose one or the other to come next, we could describe all the paths we could make with \(2^5=32\).
But we don’t. If we consider that we essentially have 5 characters, 3 R’s and 2 D’s, once we’ve picked one at any point in the sequence, our pool of remaining characters to choose is reduced by 1. For that reason, we need to use factorials to describe how many permutations of characters can exist.
Even though there are multiple R’s as well as D’s, for now we can consider them all unique elements.
To get the number of ways you can arrange 5 unique things, it’s simply \(5!=120\).
(5 factorial, e.g. 5*4*3*2*1)
However, now we have redundancies to account for. \(5!\) alone describes this:
R1 R2 R3 D4 D5
Meaning we’re counting that permutation as well as ones like this:
R3 R1 R2 D5 D4
But of course, RRRDD is the same sequence regardless. Not all the characters are actually unique. We don’t care ‘which’ R goes in which of the first three spots, or which D in the last two.
So the number of redundancies we have is equivalent to the number of ways we can permute all the R’s AND all the ways we can permute the D’s. “And” here means we need to multiply, because all the R redundancies exist for all the D redundancies.
\[3!*2!\]So now we have our total number of ways to permute 5 things, and all the redundancies we have in this case. Remember that we get 5 by adding the dimensions of the grid, 3x2. The hard work is done, now we get to do the math.
\[{(3+2)! \over 3!*2!} = {5! \over 3!*2!}\]And there’s a fun way to divide factorials that makes things a little easier when doing them by hand. Just decompose the factorials and cross out like numbers on either side! (Imagine that the overbar is crossing out the numbers)
\[{5*4*\overline{3*2*1} \over \overline{3*2*1}*2*1} = {5*4 \over 2*1} = {20 \over 2} = 10\]So there are 10 ways to build a 5-character string with three indentical R’s and 2 identical D’s. That means we have 10 paths that get us from the top left to the bottom right! Really, from any corner to its diagonal opposite. To solve this for the 20x20 grid, let’s generalize how we solved the smaller one.
We took the dimensions of the grid, which we can call \(n\) x \(m\), and took the factorial of their sum to get our total possible permutations.
\[(n+m)!\]We calculated our redundancies by finding the permutations of each set of similar moves, the same two numbers as before, and multiplying them.
\[n!*m!\]Then we accounted for redundancies by dividing them by our total. Putting it together gives us:
\[{(n+m)!} \over {n!*m!}\]Now all we need to do is plug in our numbers to get the solution below. And hey, you know what? If you made it this far, you can keep that gold star.